| France | Actualité Vu 2531390 fois
Article N°22277
Mes petits cours de math. : LES NOMBRES RELATIFS
Nous allons approfondir la notion de nombres relatifs car nous allons travailler tout au long de ce manuel sur cet ensemble lĂ .
Â
Â
Nous pouvons dire que -3 ou 0 ou 10 ou - 5,3 ou encore 2/3 sont des nombres relatifs
 Nous pouvons rajouter que  –1 ou encore –5 sont négatifs, que 5 ou 125 sont positifs, quant à 0, il est à la fois positif et négatif.
Un nombre relatif est composé d’un signe et d’une valeur absolue (toujours positive)
Dans -1, nous avons le signe – et la valeur absolue 1, dans 3, nous avons le signe + sous entendu (que l’on n’écrit généralement pas) et la valeur absolue 3.
Nous pouvons aussi remarquer que quand nous avons deux nombres relatifs négatifs, le plus petit des deux est celui qui a la plus grande valeur absolue.
Qu’est ce que l’opposé d’un nombre relatif ?
           A tout nombre x nous avons un opposé qui est -x , nous avons donc x + (-x) = 0
L’ADDITION et la soustraction DES NOMBRES RELATIFS :
           L’addition et la soustraction des nombres relatifs sont tout à fait simples et nous savons les diriger sans aucune difficulté
           Nous savons que 4 + 4 = 8.
           Il nous faut être plus prudent quand nous avons à faire à un mélange de nombres négatifs et de nombres positifs. Mais là aussi nous savons faire :
 Nous pouvons rajouter que  –1 ou encore –5 sont négatifs, que 5 ou 125 sont positifs, quant à 0, il est à la fois positif et négatif.
Un nombre relatif est composé d’un signe et d’une valeur absolue (toujours positive)
Dans -1, nous avons le signe – et la valeur absolue 1, dans 3, nous avons le signe + sous entendu (que l’on n’écrit généralement pas) et la valeur absolue 3.
Nous pouvons aussi remarquer que quand nous avons deux nombres relatifs négatifs, le plus petit des deux est celui qui a la plus grande valeur absolue.
Qu’est ce que l’opposé d’un nombre relatif ?
           A tout nombre x nous avons un opposé qui est -x , nous avons donc x + (-x) = 0
L’ADDITION et la soustraction DES NOMBRES RELATIFS :
           L’addition et la soustraction des nombres relatifs sont tout à fait simples et nous savons les diriger sans aucune difficulté
           Nous savons que 4 + 4 = 8.
           Il nous faut être plus prudent quand nous avons à faire à un mélange de nombres négatifs et de nombres positifs. Mais là aussi nous savons faire :
4 + 5 – 10 = - 1
Â
Â
En schématisant cette opération, nous trouvons :
Â
Â

Â
Notre résultat est donc le nombre relatif négatif -1
Pour nous faciliter la tâche lors d’opĂ©rations Ă rallonge, nous mettrons les positifs d’un cĂ´tĂ© et les nĂ©gatifs de l’autre :Â
3 + 5 – 8 + 6 – 4 – 3+ 7 =
3 + 5 + 6 + 7 – 4 – 3 – 8 = 21 – 15 = 6
           Deux nombres positifs multipliés entre eux, donnent un résultat positif :
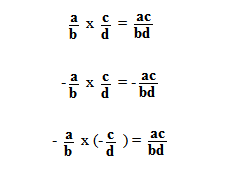
EXERCICES
Compléter avec le signe < ou le signe > :
-20....-30Â Â Â Â Â Â Â Â
-10....6Â Â Â Â Â Â Â Â Â Â Â
17....-1Â Â Â Â Â Â Â Â Â Â Â
0....-8,2Â Â Â Â Â Â Â Â Â Â
-0,1....-0,4Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â
-3,1....-2,9
3,49....3,5Â Â Â Â Â Â Â
-3,49....-3,5.
Ranger dans l’ordre croissant :
70Â ; -5Â ; 8,4Â ; -81Â ; -7,5Â ; 0Â ; -42Â ; -80Â ; 1
Tracer une droite graduée ; placer les points suivants :
+3Â ; -4Â ; -1,5Â ; +1,5Â ; -6,8Â ; -7,1
Correction
Compléter avec le signe < ou le signe > :
-20.> -30Â Â Â Â Â Â Â Â -10 <6Â Â Â Â Â Â Â Â Â Â Â Â 17 >-1Â Â Â Â Â Â Â Â Â Â Â Â 0 >-8,2Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â -0,1 > -0,4Â Â Â Â Â Â
          Â
-3,1 < -2,9Â Â Â Â Â Â 4,29 < 4,3Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â -4,29 > -4,3.
Ranger dans l’ordre croissant : 70 ; -5 ; 8,4 ; -81 ; -7,5 ; 0 ; -42 ; -80 ; 1
           8,4 ; -81 ; -80 ; -42 ; -7,5 ; -5 ; 0 ; 1. 70
a) Tracez une droite graduée ; placer les points suivants :
+3Â ; -4Â ; -1,5Â ; +1,5Â ; -6,8Â ; -7,1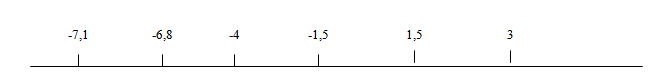
Calcule les opérations suivantes :
 (-17) + (+10) = -7
(+17) +(-10)Â Â Â = 7
 (-17) + (-13)  = -30
 (+17) + (+10) = 17
 (+7) - (-5) =   12      Â
 (+7) - (+5) =  2
 (-7) - (-5) =    -2
 (-7) - (+5) = -12
(+17) + (-4) = 13
(-6) + (-5)Â = -11
Â
Pour nous faciliter la tâche lors d’opĂ©rations Ă rallonge, nous mettrons les positifs d’un cĂ´tĂ© et les nĂ©gatifs de l’autre :Â
3 + 5 – 8 + 6 – 4 – 3+ 7 =
3 + 5 + 6 + 7 – 4 – 3 – 8 = 21 – 15 = 6
La multiplication
           La seule règle à connaître est le maniement des signes des nombres relatifs :           Deux nombres positifs multipliés entre eux, donnent un résultat positif :
Le produit de a X b donne ab
           Un nombre positif multiplié à un nombre négatif donne un nombre négatif :
Le produit a X (-b)Â donne -ab
           Deux nombres nĂ©gatifs multipliĂ©s entre eux, donnent un rĂ©sultat positifÂ
Le produit de (-a) X (-b)Â donne ab
Â
Â
Â
La division
Les règles des signes de calcul de la division sont les mêmes que celles de la multiplication :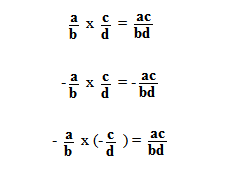
Â
A partir de maintenant, nous travaillerons dans cet ensemble R des nombres relatifs.EXERCICES
Compléter avec le signe < ou le signe > :
-20....-30Â Â Â Â Â Â Â Â
-10....6Â Â Â Â Â Â Â Â Â Â Â
17....-1Â Â Â Â Â Â Â Â Â Â Â
0....-8,2Â Â Â Â Â Â Â Â Â Â
-0,1....-0,4Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â
-3,1....-2,9
3,49....3,5Â Â Â Â Â Â Â
-3,49....-3,5.
Ranger dans l’ordre croissant :
70Â ; -5Â ; 8,4Â ; -81Â ; -7,5Â ; 0Â ; -42Â ; -80Â ; 1
Tracer une droite graduée ; placer les points suivants :
+3Â ; -4Â ; -1,5Â ; +1,5Â ; -6,8Â ; -7,1
Correction
Compléter avec le signe < ou le signe > :
-20.> -30Â Â Â Â Â Â Â Â -10 <6Â Â Â Â Â Â Â Â Â Â Â Â 17 >-1Â Â Â Â Â Â Â Â Â Â Â Â 0 >-8,2Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â -0,1 > -0,4Â Â Â Â Â Â
          Â
-3,1 < -2,9Â Â Â Â Â Â 4,29 < 4,3Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â Â -4,29 > -4,3.
Ranger dans l’ordre croissant : 70 ; -5 ; 8,4 ; -81 ; -7,5 ; 0 ; -42 ; -80 ; 1
           8,4 ; -81 ; -80 ; -42 ; -7,5 ; -5 ; 0 ; 1. 70
a) Tracez une droite graduée ; placer les points suivants :
+3Â ; -4Â ; -1,5Â ; +1,5Â ; -6,8Â ; -7,1
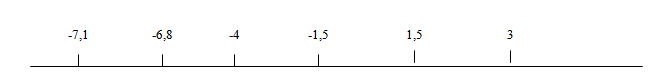
Calcule les opérations suivantes :
 (-17) + (+10) = -7
(+17) +(-10)Â Â Â = 7
 (-17) + (-13)  = -30
 (+17) + (+10) = 17
 (+7) - (-5) =   12      Â
 (+7) - (+5) =  2
 (-7) - (-5) =    -2
 (-7) - (+5) = -12
(+17) + (-4) = 13
(-6) + (-5)Â = -11
Â
Â
Â
Gaelle Laborie
Lien :?
Réagissez, commentez !
- Aucun commentaire pour l'instant
